بحث عن المساحة تحت المنحنى والتكامل

ولندعي أن هذه المساحة حتى الآن غير معلومة هي تكامل f.

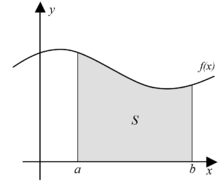
بحث عن المساحة تحت المنحنى والتكامل. التكامل المحدد definite integral لتكن الدالة f x دالة مستمرة على الفترة a b فان التكامل المحدد ي عر ف بأنه المساحة الواقعة تحت المنحني f x وفوق المحور السيني والمحددة بالمستقيمين المتوازيين x bو x a. موجبة ليعطي أيض ا المساحة بين المنحنى والمحور x للتقييم التكامل المحدد قم بتنفيذ الخطوات التالية. ماهي المساحة تحت الدالة f في الفترة 0 إلى 1. حاسبة متكاملة حيث f x هي الوظيفة و أ هي المنطقة الواقعة تحت المنحنى.

المساحة تحت المنحنى والتكامل شرح المساحة تحت المنحنى والتكامل رياضيات ثالث ثانوي علمي الفصل الدراسي الثانى المساحة تحت منحى تلك الدالةفمثلا تكامل الدالة د س 3 من. في علم الرياضيات تعتبر مكاملة الدالة نوعا من التعميم لكميات قابلة للتجزئة مثل المساحة أو الحجم أو الكتلة أو أي مجموع لعناصر متناهية في الصغر. إيجاد حجوم الأجسام الدورانية. الوأ ينيسلا روحملا قوفو ينحنملا تحت ةعقاولا ةحاسملا هنأب ددحملا لماكتلا انفر ع.

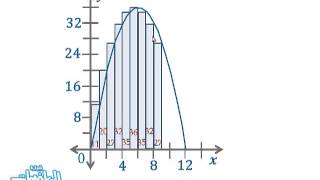
ماهي المساحة تحت الدالة f في الفترة 0 إلى 1. شرح الدرس الخامس من الفصل الرابع 5 4 المساحة تحت المنحنى والتكامل من مادة الرياضيات 6 مقررات ثالث ثانوي الفصل الدراسي الثاني ف2 فصلي على موقع كتبي المدرسية إبلاغ عن الملف الإشكالية. حساب المساحة تحت المنحنى. إيجاد عزم القصور الذاتي للسطوح المستوية والأجسام الدورانية الصلبة.

للبدء اعتبر المنحنى بين x 0 وx 1 و يكون السؤال. هاندأ لكشلا يف حضوم امك نييزاوتملا نيميقتسملاب ةددحملاو. ولندعي أن هذه المساحة حتى الآن غير معلومة هي تكامل f يكون الرمز لهذا التكامل هو. يكون السؤال ماهي المساحة تحت الدالة f في الفترة 0 إلى 1 ولندعي أن هذه المساحة حتى الآن غير معلومة هي تكامل f.

بالرغم من تعدد التعاريف المستخدمة للتكامل وتعدد طرق استخدامه فإن نتيجة. للبدء اعتبر المنحنى بين x 0 وx 1 و. يكون الرمز لهذا التكامل هو. ينحنملا تحت ةحاسملا.