بحث عن المصفوفات في الرياضيات

فمثلا المصفوفة الأولى تحتوي على ثلاثة مصفوفات وثلاث أعمدة لذا فسعتها 3x3.

بحث عن المصفوفات في الرياضيات. ضرب كل عنصر من عناصر كل صف من صفوف المصفوفة الأولى في كل عنصر من عناصر كل عمود من الأعمدة في المصفوفة الثانية. بحث عن المصفوفات في الرياضيات pdf. بحث رياضيات عن المصفوفات أنواعها واستخداماتها تعريف المصفوفات المصفوفة هي مجموعة مستطيلة من الأرقام أو الرموز الرياضيات الأخرى ويتم فيها تحديد العمليات الرياضية مثل الإضافة والضرب. عدد الصفوف الخطوط الأفقية وعدد الأعمدة الخطوط العمودية يسمى سعة المصفوفة.

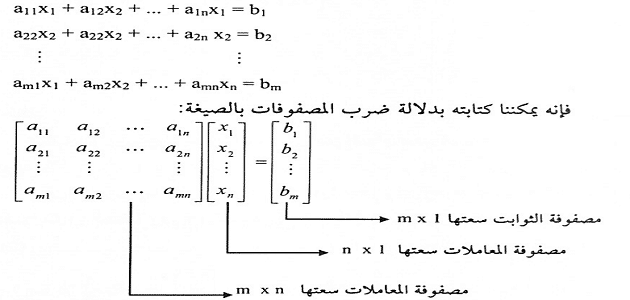
أولا يجب التحق ق من أن عدد الأعمدة في المصفوفة أ مساويا لعدد الصفوف في المصفوفة ب. الكرة والأسطوانة الدائرة وقياساتها وغيرها العديد. أهمية المصفوفات في حياتنا اليومية. في الرياضيات المصفوفة بالإنجليزية.

Matrix هي مجموعة مستطيلة من الأعداد أو من الرموز أو من التعبيرات منتظمة بشكل أعمدة وصفوف. استخدام المصفوفات كأداة للتوقع والتنبؤ لمتغيرات ما. بحث عن العمليات على المصفوفات والمحددات المصفوفات هي أحد أجزاء الرياضيات التي تم اكتشافها مثل باقي الأجزاء التي ساهمت في حل المعادلات المعقدة والتي يصعب حلها من خلال الخطوات المتعارف عليها مثل الجمع والطرح والضرب والقسمة فقد ظهرت في الرياضيات عمليات أكثر تعقيدا لابد. 1 0 0 2 2 0 1 3 0 1 2 4.

ي عرف ضرب اثنين من المصفوفات في حالة إذا كان عدد أعمدة المصفوفة الأولى مساوي ا لنفس عدد الصفوف في المصفوفة الثانية. بحث رياضيات عن المصفوفات كامل يمكننا عمله من خلال توضيح مفهوم الـ مصفوفة والمقصود بالمصفوفة جزء من الجبر المتفرع من علم الرياضيات وهي ذات شكل مستطيل تحتوي علي شكل أعمدة وصفوف من الأرقام أو التعبيرات أو الرموز. 0 0 3 2 1 0 0 3 3 1 1 4. الخطوط الأفقية للعناصر تسمى صفوفا والخطوط العمودية تسمى أعمدة.

معرفة دور المصفوفات وكيفية استخدامها في المجالات المختلفة ور البيانات عليها. فمثل ا إذا كانت هناك مصفوفة س عبارة عن مصفوفة أ ب ومصفوفة ص عبارة عن مصفوفة ب ج فإن حاصل ضرب المصفوفتين يكون الناتج عنهما المصفوفة س ص. أمثلة على المصفوفات في حياتنا ربط المصفوفات في الواقع. وهي مصفوفة مربعة يكون جميع عناصرها صفر إلى عناصر القطر الرئيسي تكون ذات قيم مختلفة.

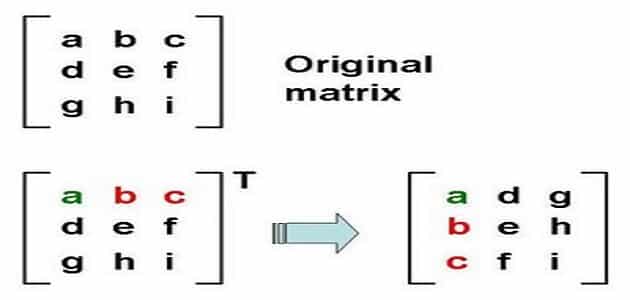
ي دعى كل عنصر من هذا المجموعة بعنصر أو مدخل للمصفوفة.